Angka Penting

Angka Penting

Angka penting adalah semua angka yang diperoleh dari hasil pengukuran. Angka penting terdiri dari atas angka pasti dan angka taksiran (angka yang diragukan) sesuai dengan alat ukur yang digunakan.

Gambar 11. Pengukuran yang membutuhkan angka taksiran

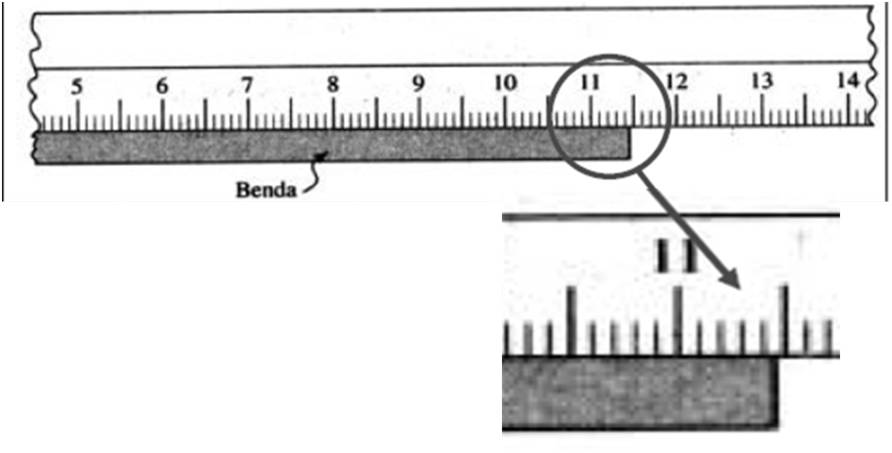
Misalnya panjang benda yang diukur ditunjukan seperti gambar 13. Pada gambar tersebut, tampak bahwa ujung benda terletak diantara angka 11,44 cm dan 11,45 cm. Sehingga, kita akanmenyatakan bahwa panjang benda yang mendekati kebenaran adalah 15,45 cm. angka terakhir, yakni angka 6 adalah angka perkiraan (taksiran), karena angka ini tidak terbaca pada skala mistar.

Aturan angka penting

1. Semua angka bukan nol adalah angka penting.

Contoh: 836,5 gr memiliki empat angka penting

2. Angka nol yang terletak di antara dua angka bukan nol termasuk angka penting.

Contoh:  75,006  Kg memiliki lima angka penting

3. Untuk bilangan desimal yang lebih kecil dari satu, maka angka nol setelah angka bukan nol termasuk angka penting.

Contoh: 0,0060 m memiliki dua angka penting

4. Untuk bilangan desimal yang lebih kecil dari satu, maka angka nol sebelum angka bukan nol tidak termasuk angka penting.

Contoh: 0,006 m memiliki satu angka penting

5. Bilangan-bilangan puluhan, ratusan, ribuan dan seterusnya yang memiliki angka nol harus ditulis dalam notasi ilmiah. Angka-angka pada notasi ilmiah merupakan angka penting.

Contoh: 8900 gr ditulis menjadi 8,9 x 10³ gr memiliki dua angka penting

Aturan Pembulatan Angka

Ketika angka-angka ditiadakan sari suatu bilangan, nilai dari angka terakhir yang dipertahankan ditentukan dengan suatu proses yang disebut pembulatan bilangan. Aturan pembulatan bilangan tersebut, antara lain:

• Angka-angka yang lebih kecil daripada 5 dibulatkan ke bawah
• Angka-angka yang lebih besar daripada 5 dibulatkan ke atas
• Angka 5 dibulatkan ke atas jika sebelum angka 5 adalah ganjil dan dibulatkan ke bawah jika angka sebelum angka 5 adalah angka genap.

Operasi-operasi dalam angka penting

1. Operasi penjumlahan dan pengurangan

Dalam melakukan operasi penjumlahan atau pengurangan, maka hasilnya hanay boleh mengandung satu angka taksiran (angka terakhir dari suatu bilangan penting).

Contoh 1:

35,572                   2 angka taksiran

  2,2626 +            8 angka taksiran

37,8346                

4 dan 6 merupakan angka taksiran, sehingga hasil penjumlahan ditulis 37,835 disesuaikan dengan atuan pembulatan.

Contoh 2:

385,617                 7 angka taksiran

  13,2     -              2 angka taksiran

372,417                

4 dan 7 merupakan angka taksiran, sehingga hasil penjumlahan ditulis 372,42 disesuaikan dengan atuan pembulatan.

2. Operasi perkalian dan pembagian

Dalam operasi perkalian atau pembagian, maka hasilnya hanya boleh memiliki angka penting sebanyak bilangan yang jumlah angka pentingnya paling sedikit.

Contoh 1:

34,231                   mengandung lima angka penting

  0,250   x              mengandung tiga angka penting

8,557750

Penulisan hasil perkalian hanya boleh mengandung tiga angka penting, sehingga hasil perkalian 8,557750 ditulis 8,56 (tiga angka penting).

Contoh 2:

46,532                   mengandung lima angka penting

200      :                  mengandung satu angka penting

0,2326

Hasil pembahian hanya boleh mengandung satu angka penting, sehingga hasil perkalian 0,2326 ditulis 0,2.

Terimakasih Kunjungannya...

Aturan Pembulatan Angka

Aturan Pembulatan Angka

Pada saat analisis data atau penulisan hasil ukur suatu saat perlu pembulatan. Pembulatan dilakukan pada saat analisis data untuk menyederhanakan hitungan, sedang pada penulisan hasil ukur dilakukan untuk memenuhi aturan penulisan hasil ukur. Pembulatan pada penulisan hasil ukur dapat dilakukan pada nilai taksiran terbaiknya dan ketidak pastiannya.

 
Pembulatan angka dimulai dari digit paling kiri. Pembulatan dilakukantahap demi tahap dari digit paling kanan menuju digit didepannya (kiri digit yang dibulatkan). 

Berikut ini aturan pembulatan angka:
1. > 0,5 angka dibulatkan keatas. Sebagai contoh 67,876 dibulatkan menjadi 67,88.
2. < 0,5 angka dibulatkan kebawah. Sebagai contoh 75,624 dibulatkan menjadi 75,62.
3. = 0,5 angka dapat dibulatkan kebawah atau ke atas. Angka 0,5 dibulatkan kebawah apabila angka didepannya merupakan angka genap, sedangkan angka 0,5 dibulatkan keatas apabila angka didepannya adalah angka ganjil. Sebagai contoh 3,425 dibulatkan menjadi 3,42. angka 5 dibulatkan kebawah karena depan angka 5 merupakan angka genap. Bilangan 79,8435 dapat dibulatkan menjadi 79,844. angka 5 dibulatkan keatas karena angka didepan angka 5 adalah angka ganjil.

Maicih... :)

hukum newton II

HUKUM NEWTON II
Gaya tarikan,dorongan,dan kombiasi kedua nya
Suatu hari haby,daffa,dan indra pergi untuk mengerjakan tugas praktek fisika dirumah haby namun ketika dijalan ada sebuah mobil mogok dan kami membantu untuk mendorong, ketika kami mendorong dengan Gaya sebesar 250N/orang untuk mendorong mobil tersebut dengan massa 250 kg dari belakang (Aksi) mobil bergerak kedepan (Reaksi)

 setelah beberapa saat kami mendorong akhirnya mobil nya hidup kembali dan kami pun melanjutkan perjalanannya.

  Akhirnya kami sampai dirumah haby dan kami langsung mengerjakan tugas nya. Ketika kami sedang mengerjakan tugas,kami melihat se orang yang sedang membawa sebuah gerobak dengan massa  70kg salah seorang menariknya dari depan dengan Gaya sebesar 100 N.

 Setelah kami mengerjakan seluruh tugasnya kami membantu seorang bapak-bapak yang sedang memotong pohon tua dipinggir jalan dengan massa sekitar 50kg kami menariknya dengan gaya sebesar 250 N (Aksi) dan pohon pun perlahan-lahan semakin kebawah dan akhirnya jatuh (Reaksi).

 Setelah semua nya selesai akhirnya kami kembali pulang kerumah untuk melanjutkan aktivitas nya masing-masing dirumah.

Hukum Newton 1

Hukum Newton I : Jika resultan gaya yang bekerja pada benda yang sama dengan nol,maka benda yang mula-mula diam akan tetap diam. Benda yang mula-mula bergerak lurus beraturan akan tetap lurus beraturan


Rumus:

 

nama lain dari newton : kelembaman atau inersia (malasan)

Contoh Dalam Kehidupan Sehari-Hari

1.Selembar uang kertas diantara dua  buah botol

 2. Hulahup yg diletakkan diantara koin dan gelas

3.Tumpukan koin yg disentil

 4.Gelas diatas selembar kertas, lalu kertas ditarik.

5.Batere ABC yg diletakkan diatas kertas lalu kertas ditarik

Contoh GLB, GLBB disertai gambarnya

Contoh GLB, GLBB Dipercepat &

GLBB Diperlambat

Sama gambarnya  coy..

Hello agan, welcome back to my blog...

Enjoy agan, lesehan aja untuk kopi biar gua yg nanganin.. masalah snake urusan agan sendiri (pajak ditanggung agan sendiri)

Contoh Gerakan GLB 

1. Gerak mobil dengan kecepatan dan percepatan tetap (gambar 1.1)
2. Gerak planet mengitari matahari (gambar1.2)
3. Pesawat melaju dengan kecepatan tetap di lintasannya (gambar1.3)
4. Kereta melaju di rel dengan kecepatan tetap (gambar 1.4)
5. bulan mengitari bumi (gambar1.5)

Gambar 1.1

Gambar 1.2

Gambar 1.3

Gambar 1.4

Gambar 1.5

Contoh Gerakan GLBB Dipercepat

1. Bersepeda di jalan menurun (gambar 2.1)
2. Apel jatuh dari pohon (gambar 2.2)
3. Air terjun (gambar 2.3)
4. Meteor yang jatuh ke Bumi (gambar 2.4)
5. Pesawat lepas landas/take off (gambar 2.5)

Gambar 2.1

Gambar 2.2

Gambar 2.3

Gambar 2.4

Gambar 2.5

Contoh Gerakan GLBB Diperlambat

1. Mendaki gunung (gambar 3.1)
2. Bola dilempar ke atas (gambar 3.2)
3. Orang mengayuh sepeda di tanjakan (gambar 3.3)
4. Pesawat yang baru mendarat/landing (gambar 3.4)
5. Mobil yang mengerem mendadak (gambar 3.5)

 

Gambar 3.1

Gambar 3.2

Gambar 3.3

Gambar 3.4

Gambar 3.5

Thank's agan udah mau mampir di blog saya...

Besaran & Satuan

BESARAN & SATUAN

·         Besaran adalah segala sesuatu yang dapat diukur, mempunyai nilai yang dapat dinyatakan dengan angka dan memiliki satuan tertentu.

·  Satuan adalah pernyataan yang menjelaskan arti dari suatu besaran.

Besaran Pokok, Besaran Turunan Dan Satuannya

Besaran pokok merupakan besaran yang dipandang berdiri sendiri dan tidak diturunkan dari besaran lain. Sampai saat ini ditetapkan 7 besaran pokok sebagai berikut :

Tabel Besaran Pokok Dan Satuannya

Besaran Pokok	Satuan
Panjang Massa Waktu Suhu Kuat Arus Listrik Kuat Cahaya Jumlah Zat	kilometer, meter, sentimeter kilogram , gram , ton tahun, hari, sekon , menit fahrenheit , kelvin , celcius ampere kandela mol

Besaran turunan ialah besaran yang diturunkan dan diperoleh dari besaran-besaran pokok. Misalkan luas didefinisikan sebagai hasilkali dua besaran panjang (yaitu panjang kali lebar). Jika satuan panjang dan lebar masing-masing adalah meter, maka besaran luas adalah besaran turunan yang mempunyai satuan meter x meter atau m2. Contoh yang lain adalah besaran kecepatan yang diperoleh dari hasil bagi jarak dengan waktu. Jarak merupakan besaran panjang yang mempunyai satuan meter, sedangkan waktu mempunyai satuan sekon. Maka besaran kecepatan merupakan besaran turunan dari besaran pokok panjang dibagi besaran pokok waktu, sehingga satuannya meter/sekon atau m/s. Berikut ini adalah beberapa contoh besaran turunan beserta satuannya.

Tabel Besaran Turunan Dan Satuannya

Besaran Turunan	Rumus	Satuan
Volume Massa Jenis Percepatan Gaya Usaha & Energi Daya Tekanan Muatan Listrik	panjang x lebar x tinggi massa/volume kecepatan/waktu massa x percepatan gaya x perpindahan usaha/waktu gaya/luas kuat arus x waktu	m3, cm3, liter kg/m3 m/s2 kg.m/s2, newton kg.m2/s2, joule kg.m2/s3, watt kg/(m.s2), pascal A.s, coulomb

Sistem satuan yang biasa digunakan pada besaran pokok dan besaran turunan asalah sistem Satuan Internasional (SI) atau biasa dikenal sebagai sistem metrik yaitu meter, kilogram dan sekon yang disingkat MKS. Selain sistem metrik yang lain adalah CGS (centimeter, gram, sekon). Adapula British Engineering System yang biasa disebut sebagai sistem FPS (foot, pound, sekon).

Tabel Satuan Internasional (SI)

Besaran		SI
Besaran Pokok	Panjang Massa Waktu Suhu Kuat Arus Listrik Kuat Cahaya	meter kilogram sekon kelvin ampere kandela
Besaran Turunan	Jumlah Zat Luas Kecepatan Volume Massa Jenis Percepatan Gaya	mol m2 m/s m3 kg/m3 m/s2 kg.m/s2, N

Pada sistem metrik, satuan yang lebih besar dan lebih kecil didefinisikan dalam kelipatan 10 dari satuan standar. Jadi 1 kilometer (km) adalah 1000 m atau 103m, 1 centimeter (cm) adalah 1/100 m atau 10-2 m dan seterusnya. Awalan “centi”, “kilo”, “mili”, dan yang lainnya dapat diterapkan tidak hanya pada satuan panjang, tetapi juga satuan volume, massa, atau metrik lainnya. Misalnya saja 1 centiliter (cL) adalah 1/1000 liter dan 1 kilogram adalah 1000 gram. Tabel 4 menunjukkan awalan-awalan metrik yang sering digunakan dalam berbagai satuan.

Besaran Skalar & Besaran Vektor

Kata vektor berasal dari bahasa Latin yang berarti “pembawa” (carrier), yang ada hubungannya dengan “pergeseran” (displacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel atau benda yang bergerak, atau juga untuk menggambarkan suatu gaya. Vektor digambarkan dengan sebuah garis dengan anak panah di salah satu ujungnya, yang menunjukkan arah perpindahan/pergeseran dari partikel tersebut.

Pergeseran suatu partikel adalah perubahan posisi dari partikel tersebut. Jika sebuah partikel berpindah dari posisi A ke posisi B, maka pergeserannya dapat dinyatakan dengan vektor AB yang memiliki anak panah di B yang menunjukkan bahwa pergeseran tersebut mulai dari A ke B (Gambar 1.a). Dengan cara yang sama, perubahan posisi partikel dari posisi B ke posisi C dapat dinyatakan dengan vektor BC (Gambar 1.b). Hasil total kedua pergeseran ini sama dengan pergeseran dari A ke C, sehingga vektor AC disebut sebagai jumlah atau resultan dari pergeseran AB dan BC.

Beberapa besaran fisis lain memiliki sifat seperti “pergeseran”, yaitu disamping mempunyai besar juga mempunyai arah. Jadi untuk menyatakan besaran fisis tersebut, disamping menyatakan nilainya, kita juga harus menyatakan arahnya. Besaran fisis seperti ini dikatakan sebagai besaran vektor. Secara umum besaran vektor adalah besaran yang mempunyai besar dan arah. Contohnya : gaya, kecepatan, percepatan, momentum, impuls, momen gaya, kuat medan listrik, dan kuat medan magnet.

Sedangkan besaran fisis yang tidak mempunyai arah dan dapat dinyatakan secara tepat hanya oleh sebuah bilangan, disebut sebagai besaran skalar. Contohnya : jarak, usaha, energi, daya, massa jenis, luas, volume, tekanan, temperatur, waktu, muatan listrik, potensial listrik, dan kapasitas. Perhitungan dengan skalar dapat dilakukan dengan menggunakan aturan aljabar biasa.

Massa jenis adalah pengukuran massa setiap satuan volume benda. Semakin tinggi massa jenis suatu benda, maka semakin besar pula massa setiap volumenya. Massa jenis rata-rata setiap benda merupakan total massa dibagi dengan total volumenya. Sebuah benda yang memiliki massa jenis lebih tinggi (misalnya besi) akan memiliki volume yang lebih rendah daripada benda bermassa sama yang memiliki massa jenis lebih rendah (misalnya air).

Satuan SI massa jenis adalah kilogram per meter kubik (kg·m^-3)

Massa jenis berfungsi untuk menentukan zat. Setiap zat memiliki massa jenis yang berbeda. Dan satu zat berapapun massanya berapapun volumenya akan memiliki massa jenis yang sama.

Satuan baku adalah satuan yang ditetapkan sebagai satuan pengukuran secara umum (internasional) karena pengukuran dengan satuan baku dapat dinyatakan dengan jelas dan dapat dipakai untuk memeriksa ketepatan suatu instrumen.
Berikut contoh dari pengukuran dengan alat ukur baku:
§ mengukur meja dengan mistar
§ mengukur suhu badan dengan termometer
§ menimbang berat badan dengan timbangan
Pengukuran di atas adalah pengukuran dengan menggunakan alat ukur baku sehingga satuannya juga baku.Satuan baku yaitu meter, kg, dan sekon.
Syarat-syarat satuan baku atau standar harus memenuhi hal-hal berikut:
1. Satuan yang ditetapkan tidak mengalami perubahan oleh pengaruh apapun,
2. Satuan tersebut harus selalu sama di mana pun dan kapan pun,
3. Satuan yang ditetapkan harus mudah ditiru oleh siapa saja yang menggunakannya.
Dari syarat itulah, pada tahun 1975 para ilmuwan di Perancis telah menciptakan suatu standar sistem satuan yang berlaku di seluruh dunia. Sistem satuan baku ini disebut dengan Satuan Internasional (SI). Sistem ini juga dapat dinamakan Sistem Metrik. Sistem metrik ini terbagi menjadi dua, yakni sistem MKS dan sistem CGS.

Terimakasih Kunjungannya...

Fb & Twitter

Notasi ilmiah

 Notasi ilmiah

Notasi ilmiah atau notasi baku merupakan penulisan bilangan dalam bentuk bilangan sepuluh berpangkat. Penggunaan notasi ilmiah ini bertujuan untuk mempermudah penulisan bilangan yang besar. Dalam notasi ilmiah, angka-angka hasil pengukuran dinyatakan dengan bilangan di antara 1 dan 10 dikalikan dengan bilangan 10 berpangkat.

Aturan penulisan hasil pengukuran dengan notasi ilmiah adalah sebagai berikut:
a. Pindahkan koma desimal sampai hanya tersisa satu angka di kiri.
b. Hitunglah banyaknya angka yang dilewati koma desimal dan gunakan angka tersebut sebagai pangkat dan 10.

Aturan Penulisan NOTASI ILMIAH Lainnya...
 
Jika bilangan tersebut sangat besar, maka yang harus kita lakukan adalah menghitung jumlah digit pada bilangan yang sangat besar tersebut, kemudian kita kurangi 1 dan hasilnya kita tuliskan sebagai n. dan bilangan a diperoleh dari bilangan yang sangat besar tersebut kita ambil digit depannya dan kita beri koma disamping digit terdepan. Misalnya menuliskan bilangan 14240000000000000000 dalam bentuk baku.
 
Kita hitung jumlah digit yang ada pada bilangan tersebut. kita dapatkan ada 20 digit. Sehingga kita tuliskan n = 19. Dan a adalah angka depannya yang diberi tanda koma. Yaitu 1,424. Sehingga, bentuk bakunya kita dapatkan
 
14240000000000000000 = 1,424 x 10¹⁹.
 
Contoh yang lainnya :
 
87120000000 = 8,712 x 10¹⁰.
90000000000000000 = 9 x 10¹⁶.
453000000000000 = 4,53 x 10¹⁴.
536500000000000 = 5,365 x 10¹⁴.
10230000000000 = 1,023 x 10¹³.
 
Jika bilangan tersebut sangat kecil (diantara 0 dan 1 atau diantara -1 dan 0), maka yang harus kita lakukan adalah menggeser tanda koma ke kanan sampai pada bilangan bukan nol yang terdekat. Banyaknya pergeseran adalah sama dengan n dikalikan dengan negative 1. Langsung saja perhatikan contoh berikut ini :
 
0,0000025 = a x 10ⁿ
 
Pertama, kita geser tanda koma tersebut kea rah kanan sampai bertemu dengan angka tak nol yang terdekat.
 
0,0000025   (angka semula)
00,000025   (pergeseran pertama)
000,00025   (pergeseran kedua)
0000,0025   (pergeseran ketiga)
00000,025   (pergeseran keempat)
000000,25   (pergeseran kelima)
0000002,5   (pergeseran keenam)
 
Sehingga didapatkan n = -6. Dan a = 2,5. Dalam bentuk baku dapat dituliskan 2,5 x 10^-6.
 
Contoh yang lain :
 
0,0301 = 3,01 x 10^-2
0,000000102 = 1,02 x 10^-7
0,009279 = 9,279x 10^-3
0,0000000000012 = 1,2 x 10^-12

Penulisan dengan notasi ilmiah atau notasi baku mempunyai kegunaan sebagai berikut:
a. Mempermudah dalam menentukan banyaknya angka penting yang terdapat pada hasil pengukuran.
b. Mempermudah dalam menentukan orde besaran yang diukur.
c. Mempermudah dalam melaksanakan perhitungan aljabar.

Dalam menentukan hasil pengukuran, harus dihindari terjadinya kesalahan paralaks. Kesalahan paralaks yaitu kesalahan baca yang terjadi akibat kurang tepatnya mata dalam melihat alat ukur. Dengan terhindarnya kesalahan, dapat menjamin ketelitian hasil pengamatan. Ketelitian didefinisikan sebagai ukuran ketepatan yang dapat dihasilkan dalam suatu pengukuran. Ketelitian pengukuran tergantung pada alat ukur yang digunakan. Alat ukur yang baik yaitu alat yang memiliki kesalahan mutlak yang kecil. Kesalahan mutlak yaitu kesalahan terbesar yang mungkin timbul dalam pengukuran. Misalnya, mistar berskala mm memiliki kesalahan mutlak pengukuran 0,1 mm. Contoh ketelitian alat ukur misalnya mistar 0,1; jangka sorong 0,01; mikrometer sekrup 0,001.

Terimakasih Kunjungannya...

Fb & Twitter